Whats 25 Percent Of 500
maxmcgregor
Sep 12, 2025 · 5 min read
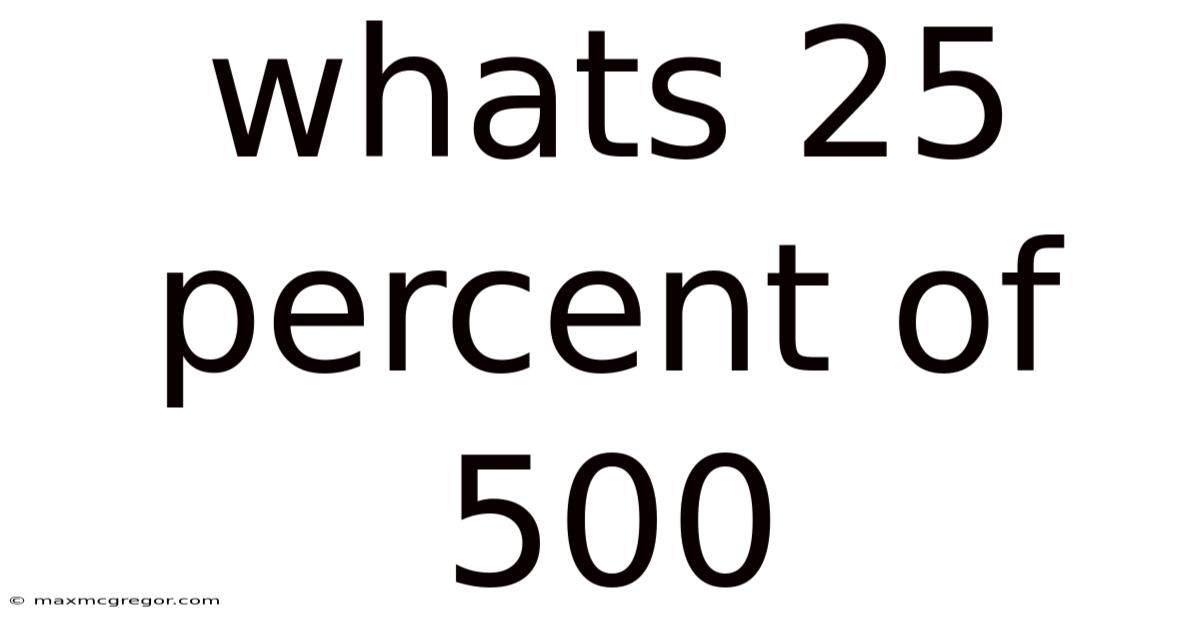
Table of Contents
What's 25 Percent of 500? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 500 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This article will not only answer the question directly but also explore the various methods to calculate percentages, their real-world applications, and delve into the underlying mathematical principles. We'll also cover some common percentage-related problems and provide you with tools to confidently tackle similar calculations in the future. By the end, you'll have a much deeper understanding of percentages beyond just a simple arithmetic operation.
Introduction: Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25. Understanding this fundamental concept is key to calculating percentages efficiently.
Method 1: Using the Fraction Method
The most straightforward method to find 25% of 500 is to convert the percentage to a fraction and then multiply:
- Convert the percentage to a fraction: 25% = 25/100
- Simplify the fraction: 25/100 simplifies to 1/4 (by dividing both numerator and denominator by 25).
- Multiply the fraction by the whole number: (1/4) * 500 = 500/4 = 125
Therefore, 25% of 500 is 125.
Method 2: Using Decimal Multiplication
Another common method involves converting the percentage to a decimal and then multiplying:
- Convert the percentage to a decimal: 25% = 0.25 (by dividing 25 by 100).
- Multiply the decimal by the whole number: 0.25 * 500 = 125
This method is often faster for those comfortable with decimal calculations. Again, the answer is 125.
Method 3: Using Proportions
The proportion method provides a more visual representation of the problem and is useful for understanding the relationship between parts and the whole. We can set up a proportion:
- Set up the proportion: x/500 = 25/100 (where 'x' represents the unknown value we're trying to find).
- Cross-multiply: 100x = 25 * 500
- Solve for x: 100x = 12500 => x = 12500/100 = 125
This method clearly shows that 25 is to 100 as x is to 500. The solution, once again, is 125.
Method 4: Using the Percentage Calculator (for complex scenarios)
While the above methods are sufficient for simple percentage calculations, more complex scenarios might benefit from using a percentage calculator. These are readily available online or as built-in functions in many spreadsheet programs like Microsoft Excel or Google Sheets. Inputting the values (25% and 500) into such a calculator will instantly provide the answer: 125.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various aspects of daily life and professional settings. Here are a few examples:
- Sales and Discounts: Calculating discounts on sale items. For example, a 20% discount on a $100 item means a saving of $20.
- Taxes: Determining the amount of sales tax or income tax payable.
- Tips and Gratuities: Calculating tips in restaurants or service industries.
- Finance and Investments: Calculating interest earned on savings accounts or investments, or determining loan repayments.
- Statistics and Data Analysis: Representing data proportions and analyzing trends. For example, expressing survey results as percentages.
- Science and Engineering: Expressing experimental results and uncertainties as percentages.
- Everyday Budgeting: Tracking expenses as percentages of income to manage finances efficiently.
Beyond the Basics: More Complex Percentage Problems
While finding 25% of 500 is a relatively straightforward calculation, let's consider more complex scenarios to further solidify your understanding:
-
Finding the original amount: If you know that 30% of a number is 60, how do you find the original number? You can set up a proportion: 30/100 = 60/x. Solving this, you get x = 200.
-
Calculating percentage increase or decrease: If a quantity increases from 100 to 125, the percentage increase is calculated as [(125-100)/100] * 100% = 25%. Similarly, a decrease from 125 to 100 represents a 20% decrease.
-
Compound interest: Compound interest calculations involve applying interest repeatedly to the principal amount plus accumulated interest. These calculations require more complex formulas.
-
Percentage points: It's important to differentiate between percentage change and percentage points. For example, an increase from 20% to 25% is a 5 percentage point increase, but a 25% increase of 20%.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate percentages?
- A: The decimal multiplication method is often the quickest and most straightforward for most calculations. However, the fraction method provides a deeper understanding of the underlying principles.
-
Q: Can I use a calculator for percentage calculations?
- A: Yes, using a calculator is highly recommended, especially for complex calculations or when dealing with large numbers.
-
Q: What if I need to calculate a percentage greater than 100%?
- A: This is perfectly possible. For example, if a quantity increases from 100 to 150, the percentage increase is 50%. This means the final quantity is 150% of the original quantity.
-
Q: How do I deal with percentages in different contexts (like taxes or discounts)?
- A: The underlying principles remain the same. You need to clearly identify the whole amount and the percentage involved in the specific context.
Conclusion: Mastering Percentages
Understanding percentages is a vital skill applicable to numerous situations. Whether it's calculating discounts, managing finances, or interpreting data, the ability to work confidently with percentages is essential. This article has explored different methods for calculating percentages, demonstrated their real-world applications, and addressed common questions. By mastering these techniques and practicing regularly, you’ll be well-equipped to handle percentage-related problems with ease and confidence. Remember, the key lies in understanding the fundamental concept of representing parts of a whole as fractions of 100, whether you use fractions, decimals, or proportions to arrive at the correct answer. So, next time you encounter a percentage problem, remember the steps outlined here and tackle it with confidence. The answer to "What's 25 percent of 500?" is unequivocally 125, but the knowledge gained extends far beyond this single answer.
Latest Posts
Latest Posts
-
What Is The Square 8
Sep 12, 2025
-
Adults Wearing Diapers For Comfort
Sep 12, 2025
-
First Time In Swinger Club
Sep 12, 2025
-
Guys Who Wear Womens Underwear
Sep 12, 2025
-
Congrats For Both Of You
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.