What Is Half Of 15
maxmcgregor
Sep 25, 2025 · 6 min read
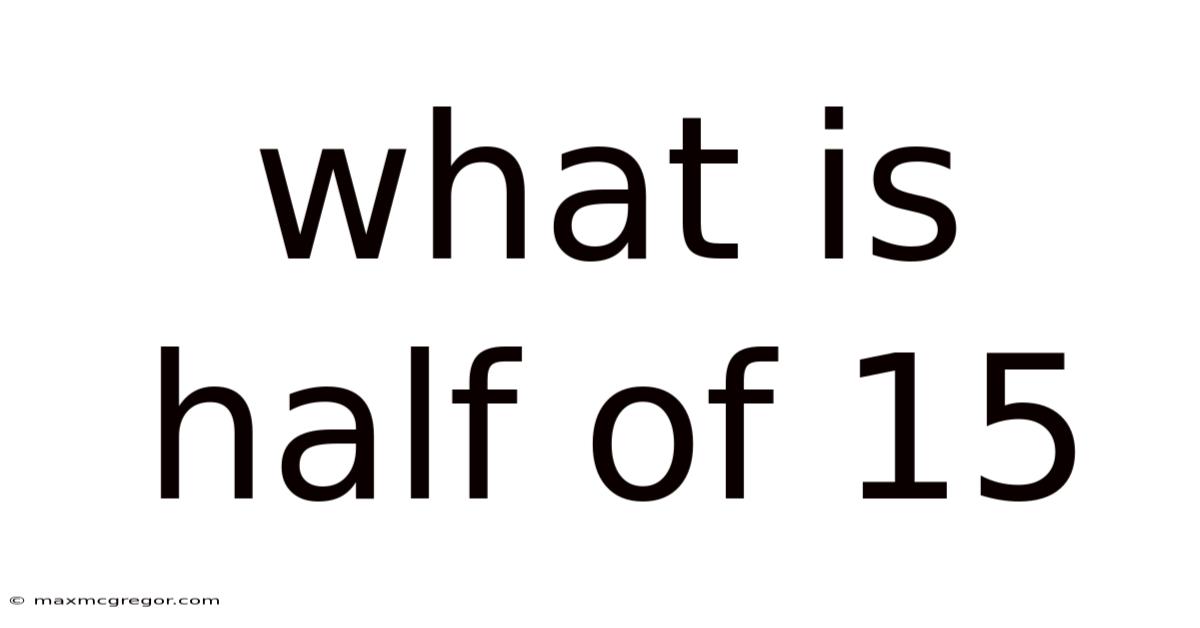
Table of Contents
What is Half of 15? A Deep Dive into Division and Fractions
Finding half of a number is a fundamental concept in mathematics, crucial for understanding fractions, division, and various real-world applications. This seemingly simple question, "What is half of 15?", opens the door to a broader exploration of mathematical principles and their practical uses. This article will not only answer the question directly but will delve into the underlying concepts, providing a comprehensive understanding for learners of all levels.
Introduction: Understanding Halves and Division
The phrase "half of 15" essentially asks us to divide 15 into two equal parts. Division is the mathematical operation that splits a quantity into a specified number of equal groups. In this case, we're dividing 15 into 2 equal groups. The result represents the size of each group, which is precisely what "half" signifies.
This simple problem can be approached in several ways, each illustrating different mathematical principles:
-
Direct Division: The most straightforward approach is to perform the division directly: 15 ÷ 2 = 7.5. This clearly shows that half of 15 is 7.5.
-
Fractions: "Half" can also be represented as the fraction 1/2. To find half of 15, we multiply 15 by 1/2: 15 x (1/2) = 15/2 = 7.5. This method emphasizes the relationship between fractions and division.
-
Visual Representation: Imagine 15 objects arranged in a row. To find half, we split the row into two equal parts. Each part contains 7.5 objects. While we can't physically have half an object, this visual approach helps conceptualize the division.
Step-by-Step Calculation: Different Methods
Let's break down the calculation process using different methods to solidify understanding:
Method 1: Long Division
For larger numbers, long division is a systematic approach. Here's how to find half of 15 using long division:
-
Set up the problem: Write 15 as the dividend (the number being divided) and 2 as the divisor (the number you're dividing by).
-
Divide: Ask yourself, "How many times does 2 go into 1?" It doesn't go into 1, so we move to the next digit.
-
Combine digits: Now ask, "How many times does 2 go into 15?" It goes in 7 times (7 x 2 = 14).
-
Subtract: Subtract 14 from 15, leaving a remainder of 1.
-
Add a decimal: Since we have a remainder, we add a decimal point to the quotient (7) and a zero to the remainder (10).
-
Continue dividing: Now ask, "How many times does 2 go into 10?" It goes in 5 times (5 x 2 = 10).
-
Final answer: The final quotient is 7.5, therefore half of 15 is 7.5.
Method 2: Fraction Multiplication
This method utilizes the fractional representation of "half":
-
Convert "half" to a fraction: "Half" is represented by the fraction 1/2.
-
Multiply: Multiply 15 by the fraction 1/2: 15 x (1/2) = (15 x 1) / (1 x 2) = 15/2
-
Convert to decimal: To get a decimal answer, divide 15 by 2: 15 ÷ 2 = 7.5
Method 3: Repeated Subtraction
This method is less efficient for larger numbers but is helpful for understanding the concept of division:
-
Start with 15: We begin with the number 15.
-
Subtract the divisor repeatedly: Subtract 2 repeatedly until you reach 0 or a number less than 2.
15 - 2 = 13 13 - 2 = 11 11 - 2 = 9 9 - 2 = 7 7 - 2 = 5 5 - 2 = 3 3 - 2 = 1
-
Count the subtractions: We subtracted 2 a total of 7 times.
-
Handle the remainder: We have a remainder of 1. To express this as a fraction, we put the remainder (1) over the divisor (2): 1/2
-
Combine the whole number and fraction: The result is 7 and 1/2, which is equal to 7.5.
Practical Applications: Real-World Examples
Understanding halves and division has countless applications in daily life:
-
Sharing equally: If you have 15 cookies and want to share them equally between two friends, each friend gets 7.5 cookies.
-
Calculating discounts: A 50% discount is equivalent to finding half the original price. If an item costs $15, a 50% discount reduces the price by $7.50.
-
Measuring ingredients: Recipes often call for half of a specific amount. Knowing how to calculate half is essential for accurate cooking.
-
Geometry: Calculating the area of a triangle involves finding half the product of the base and height.
-
Data Analysis: In statistics, finding the median often requires dividing a data set into two halves.
Further Exploration: Beyond Halves
While this article focuses on finding half of 15, the principles extend to finding other fractions or proportions of numbers. For instance:
-
One-third of 15: 15 ÷ 3 = 5
-
One-quarter of 15: 15 ÷ 4 = 3.75
-
Two-thirds of 15: 15 x (2/3) = 10
Mastering these basic concepts lays the foundation for more complex mathematical operations and problem-solving.
Frequently Asked Questions (FAQ)
Q1: Can you explain why the answer is 7.5 and not 7 or 8?
A1: Half of 15 implies dividing 15 into two equal parts. Dividing 15 by 2 gives 7.5. Choosing 7 or 8 would create unequal parts, contradicting the definition of "half."
Q2: How would you explain this to a young child?
A2: Use visual aids like cookies or toys. Arrange 15 objects and then divide them into two piles with roughly the same number in each. You'll see that it's not possible to have exactly the same number in each pile unless you cut some of the objects in half!
Q3: What if I have to find half of an odd number? Will the answer always be a decimal?
A3: Yes, when you divide an odd number by 2, the result will always be a decimal number because you can't perfectly divide an odd number into two equal whole numbers.
Q4: Are there any real-world examples where you would use fractions instead of decimals?
A4: Yes, in many cases, fractions are more practical and accurate than decimals. For example, in cooking, it's easier to measure 1/2 cup of flour than 0.5 cups. Similarly, in construction, using fractions for precise measurements is often preferred.
Conclusion: The Importance of Foundational Concepts
Finding half of 15, while seemingly trivial, embodies fundamental mathematical concepts like division and fractions. Understanding these concepts is crucial for progress in mathematics and for applying mathematical reasoning to everyday situations. This article has provided multiple methods for calculating half of 15, highlighting the interconnectedness of various mathematical approaches and demonstrating their practical significance in various contexts. By mastering these foundational skills, learners can confidently tackle more complex mathematical challenges in the future. Remember that consistent practice and a willingness to explore different problem-solving strategies are key to building a strong mathematical foundation.
Latest Posts
Latest Posts
-
Ideas For Fancy Dress Halloween
Sep 25, 2025
-
Fashion For Short Fat Women
Sep 25, 2025
-
Good Morning In Mandarin Chinese
Sep 25, 2025
-
Car Dealer Jobs Near Me
Sep 25, 2025
-
Affordable Hair Stylist Near Me
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.