What Is 70 Of 50
maxmcgregor
Sep 16, 2025 · 5 min read
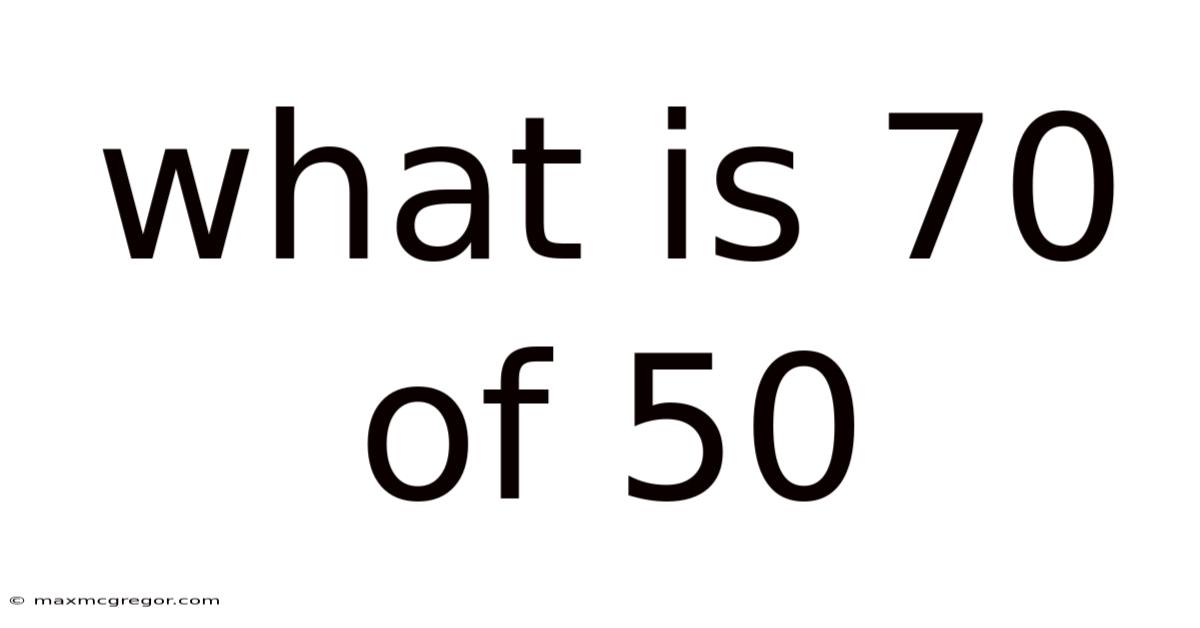
Table of Contents
What is 70% of 50? Understanding Percentages and Their Applications
This article will delve into the seemingly simple question: "What is 70% of 50?" We'll explore the calculation method, its practical applications, and broaden our understanding of percentages, a crucial concept in mathematics and everyday life. By the end, you'll not only know the answer but also possess a deeper grasp of percentage calculations and their relevance across various fields.
Understanding Percentages
Before tackling the specific problem, let's establish a firm understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For instance, 70% means 70 out of 100, or 70/100. This can also be expressed as a decimal (0.7) or a ratio (70:100). Understanding these different representations is crucial for solving percentage problems.
The fundamental formula for calculating percentages is:
(Percentage/100) * Whole Number = Part
Calculating 70% of 50: Step-by-Step Guide
Now, let's apply this knowledge to our problem: What is 70% of 50?
Step 1: Convert the percentage to a decimal:
70% is equivalent to 70/100, which simplifies to 0.7.
Step 2: Multiply the decimal by the whole number:
0.7 * 50 = 35
Therefore, 70% of 50 is 35.
Different Methods for Calculating Percentages
While the method above is straightforward, there are other approaches to calculating percentages, particularly useful for mental math or when dealing with more complex scenarios.
Method 1: Using Fractions:
- Express the percentage as a fraction: 70% = 70/100
- Simplify the fraction: 70/100 simplifies to 7/10
- Multiply the simplified fraction by the whole number: (7/10) * 50 = 35
This method is efficient when the percentage can be easily simplified into a manageable fraction.
Method 2: Using Proportions:
This method uses the concept of ratios and proportions. We can set up a proportion:
70/100 = x/50
Where 'x' represents the unknown value (70% of 50). Cross-multiplying and solving for 'x' gives:
100x = 70 * 50 100x = 3500 x = 35
This method is helpful for understanding the underlying relationship between the percentage and the whole number.
Method 3: Using a Calculator:
Modern calculators offer a percentage function that simplifies the calculation. Simply enter 70%, press the multiplication symbol, enter 50, and press equals (=). The calculator will automatically perform the necessary conversion and multiplication to provide the result (35). This is the most efficient method for speed and accuracy, particularly for more complex problems.
Practical Applications of Percentage Calculations
Understanding percentage calculations isn't confined to mathematics classrooms; it has broad practical applications in various aspects of daily life and professional fields.
-
Financial Calculations: Percentages are ubiquitous in finance. Calculating interest rates on loans or savings accounts, determining discounts on purchases, understanding tax rates, calculating tips, and analyzing investment returns all involve percentage calculations. For example, a 10% discount on a $100 item means a saving of $10 (10/100 * $100 = $10).
-
Statistical Analysis: Percentages are crucial for presenting and interpreting data in statistics. For instance, expressing survey results, analyzing market shares, or reporting the success rate of a particular treatment all rely on percentage calculations. A survey with a 70% response rate means that 70 out of every 100 people surveyed responded.
-
Scientific Research: Percentage calculations are essential in scientific research for data analysis and reporting experimental results. Expressing the concentration of a solution, calculating error margins, or representing the success rate of an experiment all require proficiency in percentage calculations.
-
Everyday Life: From calculating discounts in stores to understanding nutritional information on food labels, percentages are part of our daily encounters. A food label stating that a cereal contains 20% of the recommended daily allowance of vitamin D means that one serving provides 20 out of 100% of your recommended intake.
-
Business and Economics: Businesses use percentages constantly for profit margins, calculating costs, setting prices, analyzing sales figures, and evaluating the effectiveness of marketing campaigns. Understanding percentage change, for instance, helps track growth or decline in sales over time.
Beyond the Basics: Advanced Percentage Calculations
While our primary focus has been on finding 70% of 50, the principles extend to more complex scenarios. Let's explore some of these:
-
Calculating the Percentage: Suppose you have 35 out of 50 correct answers on a test. To find the percentage, you would use the formula: (Part/Whole) * 100%. In this case, (35/50) * 100% = 70%.
-
Finding the Whole Number: If you know that 35 is 70% of a number, you can find the original number using the formula: (Part / (Percentage/100)) = Whole. In this case, 35 / (70/100) = 50.
-
Percentage Increase/Decrease: Calculating percentage increases or decreases is important for tracking changes over time. The formula for percentage change is: [(New Value - Old Value) / Old Value] * 100%. A value increasing from 50 to 70 represents a 40% increase. Conversely, a decrease from 70 to 50 represents a 28.57% decrease.
-
Compounding Percentages: Compounding percentages involves applying a percentage change repeatedly over time. This is frequently used in finance, such as calculating compound interest.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a percentage that's not a whole number?
A: The same principles apply. For example, calculating 37.5% of 50 would involve converting 37.5% to its decimal equivalent (0.375) and multiplying by 50 (0.375 * 50 = 18.75).
Q2: Are there any online tools or calculators for percentage calculations?
A: Yes, many online calculators and tools are available that simplify percentage calculations. Simply search "percentage calculator" on a search engine.
Q3: How can I improve my understanding of percentages?
A: Practice is key. Solve various percentage problems of increasing complexity. You can find numerous practice problems online or in textbooks. Understanding the fundamental formulas and practicing with different approaches will enhance your skill and confidence.
Conclusion
This article has thoroughly explored the question "What is 70% of 50?", providing the answer (35) along with a detailed explanation of the underlying principles of percentage calculations. We've gone beyond the basic calculation to explore various methods, practical applications across diverse fields, and more complex percentage scenarios. Remember, mastering percentage calculations isn't just about solving mathematical problems; it's about acquiring a vital skill applicable in numerous aspects of life, from personal finance to professional endeavors. By understanding percentages, you equip yourself with a valuable tool for navigating the quantitative world around us.
Latest Posts
Latest Posts
-
Denim Jean Skirts Knee Length
Sep 16, 2025
-
Hunger Games Katniss Everdeen Costume
Sep 16, 2025
-
How To Become An Actor
Sep 16, 2025
-
What Do Blood Taste Like
Sep 16, 2025
-
Red Hair And Brown Eyes
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.