Integrate X 2 1 2
maxmcgregor
Sep 14, 2025 · 6 min read
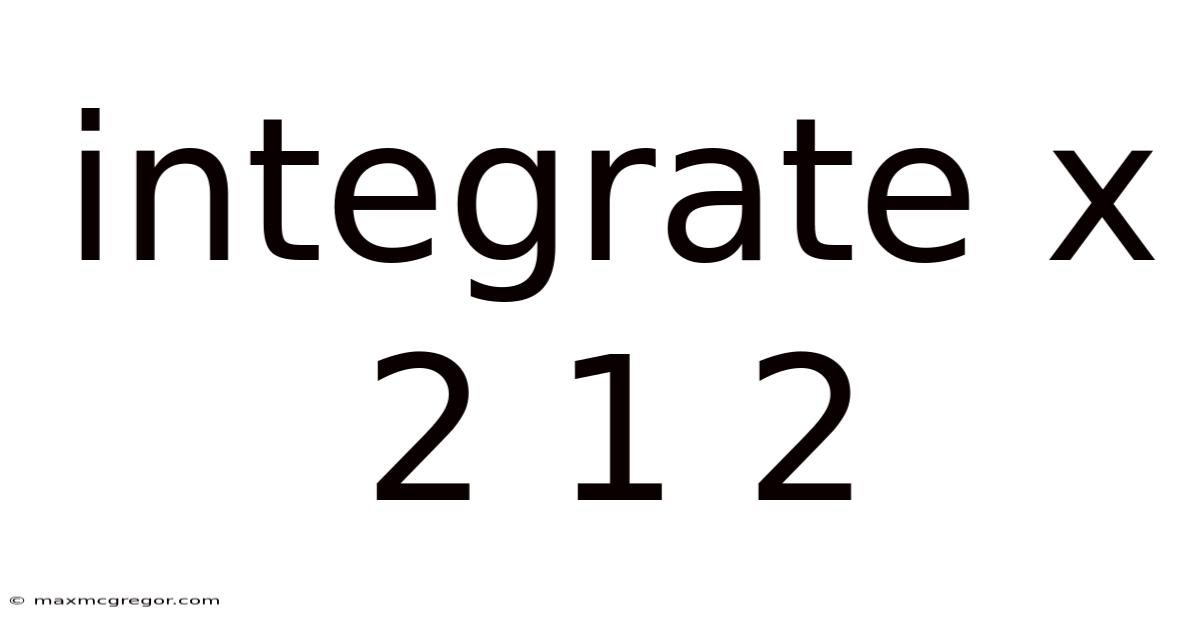
Table of Contents
Decoding the Mystery of Integrate x² + 1 / 2: A Comprehensive Guide
This article delves into the intricacies of integrating the function (x² + 1) / 2, exploring various approaches and providing a comprehensive understanding of the process. We'll move beyond a simple answer, examining the underlying principles and practical applications of integral calculus, making this concept accessible to students and enthusiasts alike. This guide covers the integration process step-by-step, explains the underlying mathematical principles, and addresses frequently asked questions. Mastering this seemingly simple integration problem forms a solid foundation for tackling more complex integrals in calculus.
Introduction: Understanding the Problem
The integral ∫(x² + 1) / 2 dx represents the process of finding a function whose derivative is (x² + 1) / 2. This seemingly straightforward problem offers a great opportunity to illustrate fundamental integration techniques and solidify your understanding of calculus. We will explore how to solve this using several methods, building confidence and comprehension. The key concepts we'll cover include power rule integration, constant multiple rule, and the significance of the constant of integration. By the end, you'll not only know the solution but also understand why the solution is correct and how it fits into the broader framework of integral calculus.
Step-by-Step Integration: The Power Rule Approach
The most straightforward approach to solving this integral involves applying the power rule of integration and the constant multiple rule. Let's break it down step-by-step:
-
Simplify the Expression: First, we simplify the integrand. We can rewrite (x² + 1) / 2 as (1/2)x² + (1/2). This makes the integration process clearer.
-
Apply the Power Rule: The power rule states that ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, where 'n' is any real number except -1, and 'C' is the constant of integration. We apply this rule to each term separately:
-
For (1/2)x², we have n = 2. Applying the power rule: ∫(1/2)x² dx = (1/2) * (x²⁺¹)/(2+1) = (1/2) * (x³)/3 = (1/6)x³
-
For (1/2), we have n = 0 (since (1/2) is equivalent to (1/2)x⁰). Applying the power rule: ∫(1/2) dx = (1/2) * (x⁰⁺¹)/(0+1) = (1/2)x
-
-
Combine the Results: Combining the integrated terms, we get:
∫(1/2)x² + (1/2) dx = (1/6)x³ + (1/2)x + C
Therefore, the indefinite integral of (x² + 1) / 2 is (1/6)x³ + (1/2)x + C. Remember, the constant of integration, C, is crucial because the derivative of a constant is always zero. Many different functions could have (x² + 1) / 2 as their derivative, differing only by the constant term.
Understanding the Constant of Integration (C)
The constant of integration, C, is a vital part of the solution and often overlooked by beginners. It represents the family of functions that share the same derivative. Consider the functions:
- f(x) = (1/6)x³ + (1/2)x
- g(x) = (1/6)x³ + (1/2)x + 5
- h(x) = (1/6)x³ + (1/2)x - 2
The derivatives of f(x), g(x), and h(x) are all identical: (x² + 1) / 2. The constant C accounts for this ambiguity. Only when we have definite limits of integration (a and b in ∫ₐᵇ f(x) dx) does the constant C cancel out.
Alternative Approaches: Linearity of Integration
The linearity of integration allows us to break down the problem into simpler parts. This property states that the integral of a sum (or difference) of functions is the sum (or difference) of their integrals. We can use this to solve our problem in a slightly different way:
∫(x² + 1) / 2 dx = (1/2) ∫(x² + 1) dx = (1/2) [∫x² dx + ∫1 dx]
Applying the power rule to each integral separately:
= (1/2) [(x³)/3 + x] + C = (1/6)x³ + (1/2)x + C
This demonstrates the flexibility and power of the linearity property.
Definite Integration: Adding Limits
While indefinite integration gives us a family of functions, definite integration provides a numerical answer. If we were to evaluate the definite integral of (x² + 1) / 2 from, say, x = 0 to x = 2, we would proceed as follows:
-
Find the indefinite integral: As determined previously, this is (1/6)x³ + (1/2)x + C.
-
Evaluate at the upper and lower limits: We substitute the upper limit (x = 2) and the lower limit (x = 0) into the indefinite integral:
[(1/6)(2)³ + (1/2)(2)] - [(1/6)(0)³ + (1/2)(0)] = (8/6) + 1 = 7/3
Therefore, the definite integral of (x² + 1) / 2 from 0 to 2 is 7/3. Note that the constant of integration, C, cancels out during this process.
Practical Applications: Real-World Significance
The seemingly simple integration of (x² + 1) / 2 has numerous applications across various fields:
-
Physics: Calculating displacement from an acceleration function often involves integrating twice. If acceleration is represented by a quadratic function, similar integrals appear.
-
Engineering: Determining the area under a curve, crucial in structural analysis and fluid dynamics, frequently uses integration. The function (x² + 1) / 2 could represent a simplified model of a pressure profile.
-
Economics: Calculating total cost from a marginal cost function involves integration. Marginal cost functions can sometimes be approximated by quadratic functions.
-
Statistics: Calculating expected values and variances often involves integration over probability density functions.
Frequently Asked Questions (FAQ)
-
Q: What if the numerator was different? A: If the numerator were different, say 3x² + 5, you would still apply the power rule and constant multiple rule to each term separately. The process remains similar but with different coefficients.
-
Q: Can I use other integration techniques? A: While the power rule is the most efficient method for this specific problem, more advanced techniques like u-substitution or integration by parts become necessary for more complex integrals.
-
Q: Why is the constant of integration so important? A: The constant of integration accounts for the fact that many functions can share the same derivative. It represents the family of antiderivatives. Without it, the solution is incomplete.
-
Q: How can I check my answer? A: The easiest way to verify your integration is by differentiating the result. If the derivative matches the original integrand, your integration is correct.
-
Q: What if the integral is definite? A: With definite integrals, you evaluate the indefinite integral at the upper and lower limits of integration, subtracting the result at the lower limit from the result at the upper limit. The constant of integration cancels out in this process.
Conclusion: Mastering the Fundamentals
Integrating (x² + 1) / 2, while seemingly simple, provides a crucial stepping stone in understanding the fundamental principles of integral calculus. By mastering this basic integral, you'll be better equipped to tackle more complex problems involving the power rule, constant multiple rule, and the significance of the constant of integration. Remember to practice consistently, explore different approaches, and always verify your solutions. The journey to mastering calculus is a rewarding one, and this simple problem serves as a great starting point. This comprehensive guide helps solidify your understanding, providing a strong base for further explorations in the fascinating world of integral calculus. Keep practicing, and you will find your skills growing exponentially.
Latest Posts
Latest Posts
-
How Long Is A Moment
Sep 14, 2025
-
Football Boots With A Sock
Sep 14, 2025
-
Towns That Start With Z
Sep 14, 2025
-
Birthday Quotes For Son Birthday
Sep 14, 2025
-
Is Adhd A Learning Difficulty
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Integrate X 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.